
이번 문제는 연속 펄스 부분 수열의 합 문제이다.
먼저 펄스 수열이 무엇인지 부터 살펴보자.
문제에서 정의된 펄스 수열이란 [1, -1, 1, -1 ...] 또는 [-1, 1, -1, 1..] 과 같이 1 또는 -1로 시작하면서 1과 -1이 번갈아 나오는 수열을 말한다.
연속 펄스 부분 수열이란 어떤 수열의 연속 부분 수열에 같은 길이의 펄스 수열을 각 원소끼리 곱하여 만든 수열이다.
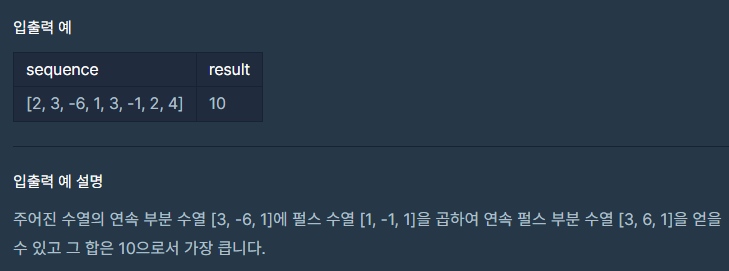
입출력 예 를 통해 정확한 개념을 집고 넘어가자
먼저 전달받은 수열에서 연속 부분 수열을 만들 수 있는 경우는 굉장히 많다.
이 중 합을 가장 크게 만들어야 하기 때문에, 단순하게 생각하면 가장 작은 수는 -1 을 곱해주고, 가장 큰 수는 +1 을 곱해주는것이 가장 현명한 방법으로 보인다.
한가지 유의해야 할 점은 펄스 수열의 짝수, 또는 홀수 index 가 양수, 음수로만 구성되기에 그 부분만 조심해 주면 될것 같다.

첫번째 작성한 코드이다.
정확하게 10문제만 통과이고, 나머지는 시간초과에 걸린다
어느정도 예상은 했지만, 해당 코드를 작성하고 나니 dp로 풀이가 가능할 것 같은 예감이 든다.
입출력 예 1번을 위 코드로 돌려보면 [[-6, 6], [8, -8], [5, -5], [1, -1], [2, -2], [1, -1], [2, -2], [-4, 4]] 의 sub_t 값을 얻을 수 있다.
여기서 한가지 중요한 사실은 +1 이나 -1 이나 시작값을 설정해도 결과적으로 절대값은 같음을 알 수 있다.
즉, 굳이 시작값을 -1로 할지 1로 할지 고민하지 않아도 될 문제처럼 보인다.

좀더 간결하게 구현하기 위해 구글링을 참조하였다.
위 코드를 이용하면 [0, 2, -1, -7, -8, -5, -4, -2, -6] 의 sub_t 값을 얻을 수 있으며, 이는 각 구간에 대한 누적합이 된다.
여기에서 한가지 중요한 사실은 펄스 수열을 곱하기 때문에 최대값은 언제나 양수, 최소값은 언제나 음수가 된다.
즉 최대값 - 최소값은 절대 음수가 될 수 없다. 무조건 양수가 된다.
그렇다면 반대로, 위 코드의 반복문을 1을 시작점으로 하게 되면 최대값과 최소값 역시 반대로 뒤집어 진다는 결론이 나온다.
[0, 2, -1, -7, -8, -5, -4, -2, -6] 의 sub_t를 다시 살펴보자
생성 당시에 n+1 만큼 생성하였기 때문에 sub_t[i] 는 sequence[:i+1] * 펄스 수열 의 누적값이 된다.
즉 sub_t 의 특정 구간의 값을 구하고 싶은 경우라면, 반대로 범위의 시작과 끝 부분의 값의 차가 된다.
(즉 sequence[2] ~ sequence[5] 의 부분합은 sub_t[6] - sub_t[3] 이 된다.)
이를 이용하여 누적합의 최대값이 되는 지점과 최소값이 되는 지점의 차가 해당 수열의 연속 펄스 수열의 최대합이 된다.

'프로그래머스 퀴즈(Python) > level 3' 카테고리의 다른 글
| 23.07.14 파이썬 코딩 퀴즈#266 2차원 동전 뒤집기 (프로그래머스 스쿨) (0) | 2023.07.14 |
|---|---|
| 23.05.23 파이썬 코딩 퀴즈#245 아방가르드 타일링(프로그래머스 스쿨) (0) | 2023.05.23 |
| 23.05.19 파이썬 코딩 퀴즈#243 인사고과 (프로그래머스 스쿨) (1) | 2023.05.19 |
| 23.05.13 파이썬 코딩 퀴즈#242 표 병합 (프로그래머스 스쿨) (1) | 2023.05.13 |
| 23.05.11 파이썬 코딩 퀴즈#241 미로 탈출 명령어 (프로그래머스 스쿨) (0) | 2023.05.11 |



