
이번 문제는 숫자 타자 대회 문제이다.

대회 참가자 민희는 왼손 엄지는 4, 오른손 엄지는 6의 위치에서 시작하며, 주어진 문자열 numbers를 최소한의 시간으로 타이핑하는 경우의 가중치를 구해야 한다.
가중치는 아래와 같다.
1. 이동하지 않고 제자리에서 누르는 것은 가중치 1로 계산한다.
2. 상하좌우 인접한 숫자로 이동하여 누르는 것은 가중치 2로 계산한다.
3. 대각선 인접한 숫자로 이동하여 누르는 것은 가중치 3로 계산한다.
4. 손가락은 누른 숫자의 위에서 멈춘다.

입출력 예 1번을 살펴보자.
먼저 왼손 엄지가 4 -> 1로 이동하여 누르면 가중치는 2 이다.
그 다음 7번의 경우 1 - > 4 - > 7 로 이동하게 되는데, 이동에도 가중치는 2가 소모되며, 이때 가중치는 4이다.
이제 오른손 엄지를 이용하여 6->5 로 이동하여 누르면 가중치는 2가 된다.
다시 5-> 6로 이동하여 누르면 가중치는 2이고, 이 때 최소 가중치는 10이다.
즉 이동을 하는 경우에도 가중치는 똑같이 계산된다.
코드를 작성하기에 앞서 한가지 의문점이 생겼다.
만약 왼손,오른손의 가중치가 같은 경우라면, 어떤 손을 사용해야 하는가에 대한 문제이다.
여러가지 글들과 질문게시판을 확인한 결과... 모든 경우의 수를 다 확인해 보아야 한다.
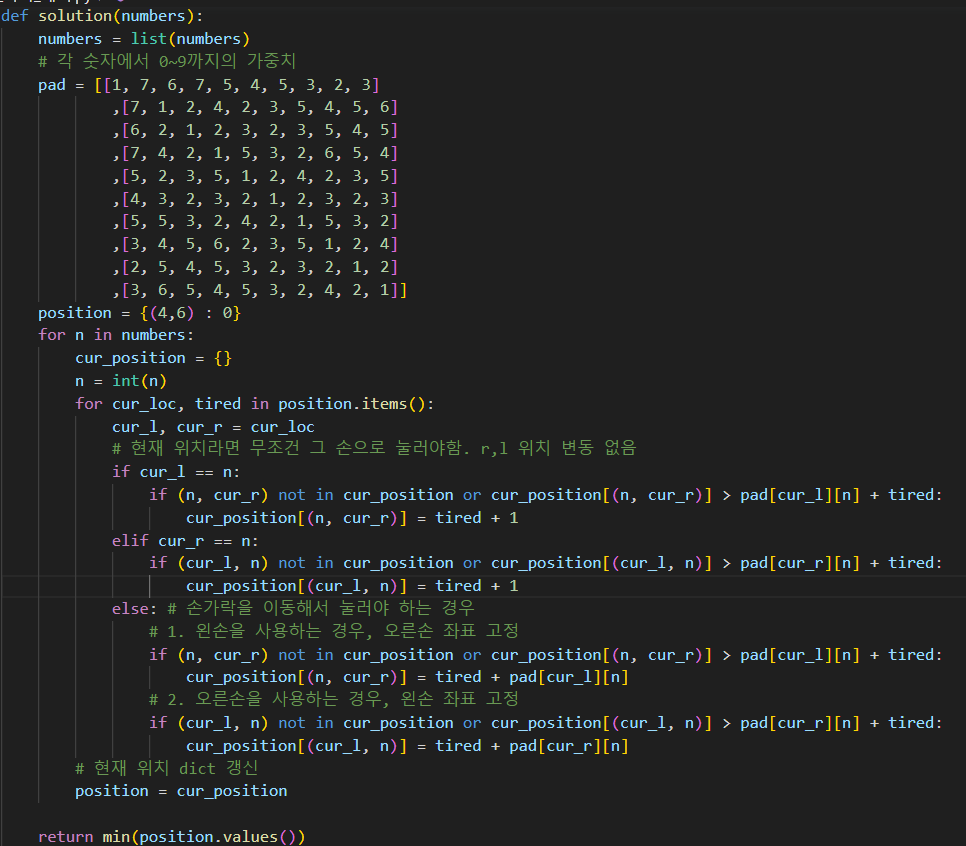
해당 문제를 풀기 위해 dp 를 이용하였는데, 이 dp의 경우 매번 갱신되는 특징이 있다.
먼저 pad 의 경우 i 위치에 따른 가중치 값들을 미리 입력하여 두었다.
즉 pad[0][2] 의 값은 0번 위치에서 2번을 누르는 가중치 가 된다.
이제 본문 코드를 살펴보면, list() 로 변환된 numbers를 돌면서 각 n 에 대하여 값을 확인하게 된다.
시작은 (4,6) 이며, 시작할때 가중치는 0 이된다.
그리고 다시 반복문으로 position 을 돌게 되는데, position 을 기준으로 매번 새롭게 만들어지는 cur_position 으로 갱신된다.
만약 눌러야 하는 번호 n 이 왼손 또는 오른손의 현재 위치이고, cur_position 에 값이 없거나, 값보다 작다면 갱신하여 주면 된다.
그리고 손가락을 이동하여 눌러야 하는 경우라면, 하나의 cur_loc 에 대하여 양 손을 사용하는 경우를 상정하여 cur_position 에 값을 넣어 주어야 한다.
입출력 예 1번 "1756" 을 예로 들면,
시작 위치는 (4,6) 이고, 이 경우 손가락 이동이 필요하기 때문에 cur_position의 key는 (1,6)과 (4,1) 두가지가 전달된다.
그리고 다음 7번을 누를때에는 (1,6)을 기준으로 (1,7)과 (7,6), (4,1)을 기준으로 (4,7)과 (7,1) 총 4개의 keys 를 가진 cur_position 이 되며, 다시 5를 누를때에는
(5,6), (7,5), (5,7), (1,5), (5,1), (4,5) 총 6가지 keys 를 가지게 된다. (중복된 keys 중 값이 작은 값으로 갱신된다.)
최종적으로 (5,6),(6,5),(7,6),(6,7),(1,6),(6,1),(4,6) 7개의 keys를 가진 cur_position 이 완성된다.
이중 필요한 것은 values()의 최소값이므로, 이를 min()을 이용하여 추출 후 반환하면 된다.

개인적으로 어떻게 코드를 풀어야 할 지, 머릿속으로는 그려졌는데, 이를 코드로 구현하기 까지 상당한 시간이 소요되었다.
dp 개념을 오직 리스트로만 생각하다보니, 매번 갱신이 필요한 가중치 값을 좌표를 이용해 deque()로 풀어보고자 했던 점을 반성해야 겠다.
'프로그래머스 퀴즈(Python) > level 3' 카테고리의 다른 글
| 23.05.11 파이썬 코딩 퀴즈#241 미로 탈출 명령어 (프로그래머스 스쿨) (0) | 2023.05.11 |
|---|---|
| 23.05.10 파이썬 코딩 퀴즈#240 억억단을 외우자 (프로그래머스 스쿨) (0) | 2023.05.10 |
| 23.05.08 파이썬 코딩 퀴즈#238 등대 (프로그래머스 스쿨) (0) | 2023.05.08 |
| 23.05.03 파이썬 코딩 퀴즈#237 부대복귀 (프로그래머스 스쿨) (0) | 2023.05.03 |
| 23.04.27 파이썬 코딩 퀴즈#236 고고학 최고의 발견 (프로그래머스 스쿨) (0) | 2023.04.27 |



