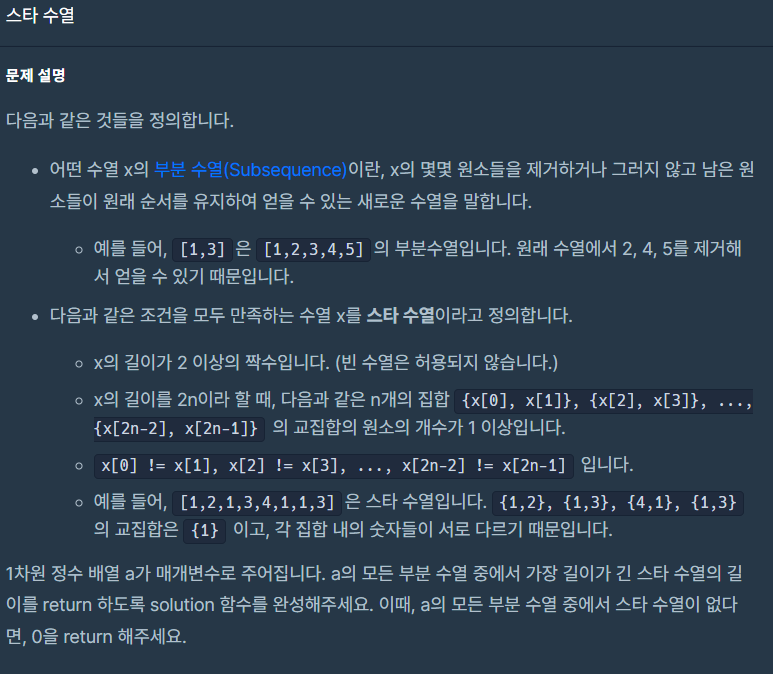
이번 문제는 스타 수열 문제이다.
먼저 스타 수열과 부분 수열이 무엇인지에 대한 이해가 필요하다.
부분수열이란 어떤 수열 x의 몇몇 원소를 제거하거나 그러지 않고 남은 원소들이 원래 순서를 유지하여 얻을 수 있는 새로운 수열을 의미한다.
그리고 스타 수열이란 다음 조건을 만족하는 수열 x를 스타 수열이라고 정의할 수 있다.
1. x 의 길이는 2이상의 짝수이다. (빈 수열 x)
2. x 의 길이가 2n 이라고 할때, 다음과 같은 n개의 집합 {x[0],x[1]}, {x[2],[3]} ... 의 교집합의 원소의 개수가 1 이상이다.
3. 또한 x[0] != x[1] 이고 x[1] != x[2] 이다. 하지만 x[0] == x[2] 는 가능하다. (교집합의 원소의 개수가 1 이상이다.)
그리고 전달받은 1차원 정수 배열 a를 확인하여 a의 모든 부분 수열 중에서 가장 길이가 긴 스타 수열의 길이를 return 해야 한다. 만약 스타 수열이 없다면 0 이다.

이제 입출력 예제를 살펴보자
입출력 예 1은 길이가 1 이기 때문에 스타수열이 아니다. 따라서 0를 반환한다
입출력 예 2는 전체 길이가 6이다.
먼저 전체 배열을 두쌍씩 짝을 지어 나누면 {5,2},{3,3},{5,3} 가 나온다. x[0] != x[1] 의 규칙과 세 집합 사이의 교집합이 없기에 스타 수열이 아니다. 이제 값을 제거하여 부분 수열을 확인해 보아야 한다.
짝수 배열만 가능하기에 2개의 값을 제거해야 한다. 그리고 최종적으로 길이가 4이고 집합을 2개를 만들어야 한다.
교집합도 생각해야 하기에 2개를 제거했을때 최소한 한 요소가 2개느느 남아야 한다.
따라서 (2,3) 또는 (3,3)을 제거 할 수 있다.
제거하고 남겨진 부분 수열은 [5,3,5,3] 과 [5,2,5,3] 이다. 두 수열 모두 조건을 만족하므로 수타 수열이며, 이때 최대 길이는 4가 된다.

이 문제는 생각보다 빠르게 풀었다.
먼저 sort_n 에는 각 요소별로 개수를 저장한다. 그 다음 다시 base_n 에 리스트로 저장해 준 다음 개수 기준 내림차순 정렬해 주었다.
이제 a 배열에서 개수가 가장 많은 것을 기준으로 쌍을 지어 집합을 만들면 된다.
case 는 기준값을 기준으로한 배열의 길이가 된다. 2씩 증가된다.
temp 는 a에서 순서대로 2개의 요소를 뽑아서 조건에 만족하는지를 확인하기 위해 사용한다.
이제 반복문을 통해 a 순열에서 순서대로 2개씩 temp 에 전달한다. 만약 조건을 만족한다면 case 값을 2 증가 시키고, temp 는 다시 비워준다.
만족하지 않는다면 값을 하나 제거해주면 된다.
처음에는 어떤 값을 제거해야 할지 굉장히 막막했다. 하지만 다시 생각해보면 조건문에서 해답을 얻을 수 있었다.
스타 수열이 가능한 조합은 2개를 쌍으로 지었을 때, 두개의 값이 다르고, 교집합 요소를 포함해야 한다.
반대로 얘기하면 두개의 값이 같거나, 교집합 요소를 포함하지 않는 경우이다.
두개의 값이 같다면, 두 값중 아무값이나 제거해도 상관이 없다. 그리고 만약 두개의 값이 설정한 기준값이라해도 하나를 제거해도 무넺가 없다.
만약 두 개의 값은 다르나 기준값이 존재하지 않는다면, 이 역시 어떤 값을 제거해도 무방하다.
그리고 최종적으로 생성된 case 값을 answer 과 비교하여 기존 값보다 큰 경우라면 갱신해주고, 작다면 바로 break로 탈출해주면 된다.
예를 들어 전달 받은 a 가 [0, 0, 3, 1, 2, 1, 3, 4, 0, 1, 4] 라고 가정하면, base_n 을 정렬하면 [[0, 3], [1, 3], [3, 2], [4, 2], [2, 1]] 이 된다. 따라서 시작은 0을 기준으로 시작하게 된다.

위 코드로 실행하면 최종적으로 {0,3},{1,0} 을 이용하여 스타 수열을 만들 수 있다.
그 다음 값은 1 이다.

1을 기준으로 하면 {0,1},{2,1},{3,1} 을 이용하여 스타 수열을 만들 수 있다.
원소의 개수가 3개라면 만들 수 있는 집합은 3개 이며, 총 길이는 6이다. 따라서 최대값이 되었다.
바꾸어 말해 그 밑으로는 값을 확인 할 필요가 없다는 점이다.

'프로그래머스 퀴즈(Python) > level 3' 카테고리의 다른 글
| 23.03.29 파이썬 코딩 퀴즈#205 광고 삽입(프로그래머스 스쿨) (0) | 2023.03.29 |
|---|---|
| 23.03.28 파이썬 코딩 퀴즈#204 합승 택시 요금(프로그래머스 스쿨) (0) | 2023.03.28 |
| 23.03.22 파이썬 코딩 퀴즈#202 풍선 터트리기 (프로그래머스 스쿨) (0) | 2023.03.22 |
| 23.03.21 파이썬 코딩 퀴즈#201 경주로 건설 (프로그래머스 스쿨) (0) | 2023.03.21 |
| 23.03.17 파이썬 코딩 퀴즈#200 보석 쇼핑 (프로그래머스 스쿨) (0) | 2023.03.17 |



